[BOJ] 1655 가운데를 말해요

 

https://www.acmicpc.net/problem/1655

1655번: 가운데를 말해요

 

이제까지 입력된 숫자 중 중앙값을 출력하는 문제.

 

 

1/ 조건

1) 여러 개의 정수가 입력된다. 수가 입력될 때마다 그때까지 입력된 수 중에서 중앙값을 출력해야 한다. 만약 입력된 수가 2k(단, k는 자연수)개라면 k번째로 큰 수를 출력해야 한다.

2) 입력 첫 줄에는 입력되는 수의 갯수 n이 주어진다. 1 <= n <= 100,000.

3) 그 뒤 n줄에 거쳐 중앙값을 찾아야 하는 정수들이 한 줄에 하나씩 입력된다. -10,000 < = num <= 10,000.

4) 제한시간은 0.5초.

 

 

2/ 설계

당연하게도 입력과 정렬을 반복하는 방식은 불가능하다. 제한시간이 너무 짧으므로. O(nlogn)에 해당하는 자료구조나 알고리즘을 써야 했다. 그런데 중앙값을 가리키는 자료구조나 알고리즘이 떠오르지 않았다. 내가 아는 한 없었다. 둘 이상의 자료구조/알고리즘을 혼합해야 하는 문제로 여겨졌다.

생각은 거기까지였다. 조금 더 고민한 뒤 구글링해서 힌트를 봤다.

─최대힙과 최소힙의 조합.

이제까지 입력된 숫자들이 정렬된 1차원 배열을 상상하자. 그 가운데에는 중앙값이 있고, 우리는 그 중앙값을 아는 상황이라고 하자. 새로운 수가 입력됐다. 우리는 입력된 수가 중앙값보다 큰지 작은지 판별할 수 있고, 그 입력값을 중앙값의 왼쪽에 넣을지 오른쪽에 넣을지 또한 알 수 있다. 

이제 입력값을 어느 쪽에 넣느냐에 따라 중앙값이 달라질 것이다. 그러나 새로운 중앙값의 후보는 결국 이전 중앙값과 이전 중앙값의 양옆에 있는 숫자뿐이다.

주어진 숫자가 짝수 개일 때 다음과 같은 그림을 생각할 수 있다.

 

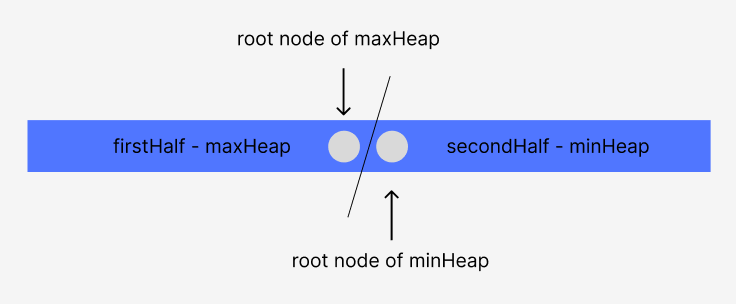
양분된 부분 중 전반부를 최대힙으로, 후반부를 최소힙으로 구성하면 최대힙의 루트 노드가 문제에서 요구하는 중앙값임을 알 수 있다. 만약 새로운 입력값이 중앙값보다 작거나 같다면? 중앙값은 변하지 않는다. 새로운 입력값이 중앙값보다 크다면? 후반부 최소힙의 루트 노드가 새로운 중앙값이 된다. 이 경우에는 최소힙의 루트 노드를 떼어다가 전반부에 붙여주어 길이의 균형을 맞춰주도록 한다. 비슷한 과정을 주어진 숫자가 홀수 개일 때도 반복할 수 있다.

 

 

3/ 구현

import java.io.*;
import java.util.PriorityQueue;
import java.util.Collections;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));

        // 예외 처리를 위하여 처음 두 입력값을 적절히 전반부와 후반부에 배치하고 중앙값을 출력하는 작업
        int n = Integer.parseInt(br.readLine());
        int first = Integer.parseInt(br.readLine());
        bw.write(first+"\n");
        int second = Integer.parseInt(br.readLine());
        if (first > second) {
            int tmp = first;
            first = second;
            second = tmp;
        }
        bw.write(first+"\n");

        // 최소힙과 최대힙을 사용하기 위해 해당 자료구조가 구현된 PrioritiyQueue 클래스를 사용
        PriorityQueue<Integer> firstHalf = new PriorityQueue<>(Collections.reverseOrder());
        PriorityQueue<Integer> secondHalf = new PriorityQueue<>();
        firstHalf.offer(first);
        secondHalf.offer(second);

        // 전반부의 마지막 원소(=최대힙의 루트 노드)가 중앙값이 되도록 재배치하는 것이 목표
        // 전반부의 마지막 원소와 입력값을 비교하여 입력값의 위치를 정하되,
        // 전반부와 후반부의 길이를 비교하여 중앙값의 위치를 재조정한다
        int num, mid;
        int len1 = 1;
        int len2 = 1;
        for (int i = 2; i < n; i++) {
            num = Integer.parseInt(br.readLine());
            if (num <= firstHalf.element()) {
                firstHalf.offer(num);
                len1++;
                if (len1 > len2+1) {
                    mid = firstHalf.remove();
                    secondHalf.offer(mid);
                    len1--;
                    len2++;
                }
            }
            else {
                secondHalf.offer(num);
                len2++;
                if (len1 < len2) {
                    mid = secondHalf.remove();
                    firstHalf.offer(mid);
                    len1++;
                    len2--;
                }
            }
            bw.write(firstHalf.element()+"\n");
        }

        br.close();
        bw.close();
    }
}

 

 

4/ 결과

야호!

 

 

5/ 한 번 더?

초기 작업과 전반부와 후반부의 길이를 재조정하는 작업이 더 간단해질 수 있을 것 같았다. 다른 사람의 풀이를 염탐했다. 과연 좋은 풀이가 있어서 바로 참고했다.

import java.io.*;
import java.util.PriorityQueue;
import java.util.Collections;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));

        int n = Integer.parseInt(br.readLine());

        PriorityQueue<Integer> firstHalf = new PriorityQueue<>(Collections.reverseOrder());
        PriorityQueue<Integer> secondHalf = new PriorityQueue<>();

        // 입력값을 전반부와 후반부에 번갈아가면서 넣되, 각 루트 노드를 매번 재배치한다.
        int num, maxVal, minVal;
        for (int i = 0; i < n; i++) {
            num = Integer.parseInt(br.readLine());
            if (i%2 == 0) firstHalf.offer(num);
            else secondHalf.offer(num);

            if (i > 0 && firstHalf.element() > secondHalf.element()) {
                maxVal = firstHalf.remove();
                minVal = secondHalf.remove();
                firstHalf.offer(minVal);
                secondHalf.offer(maxVal);
            }
            bw.write(firstHalf.element()+"\n");
        }

        br.close();
        bw.close();
    }
}

 

훨씬 깔끔한 풀이다.

 

 

6/ 후기

1) Java에 익숙해지는 데에 있어선 아쉬운 문제 및 풀이였다고 생각한다. 우선순위 큐를 써본 건 좋지만 그럴 거라면 다익스트라가 더 낫지 않았을까 싶기도.

 

2) 그래도 두 개의 자료구조를 혼합한다는 점에서 경이감의 맥락에선 굉장히 즐거운 문제였다. 앞으로도 이런 문제를 만나게 되겠지.

 

3) 내 풀이에서 고친 풀이로 나아가기 위해선 어떤 체크리스트가 필요할까? 역설계는 어렵지 않다. 한 개의 원소만 집어넣을 거라면 결국 잘 배치되었거나 잘 배치되지 않았거나 둘 중 하나고, 잘 배치되었다면 변화가 없으며 잘못 배치되었다면 그것이 루트 노드에 위치할 것이므로 비교하여 교체하면 끝. 최소힙과 최대힙의 길이 조절은 번갈아가며 삽입하는 것으로 해결…….

이렇게 사후 분석을 하면 간단해보이지만 사전에는 도달하기가 힘들다. 설계 단계에서 언급한 내용을 보다 단계적이고 명시적으로 표현했다면 저 발상에 닿았을지도 모르겠다고는 생각하지만 이는 후견지명에 불과하다. 어떤 모티베이션이 있어야 할까. 그냥 이런 식으로 수집하는 게 전부는 아닐 텐데.

 

4) 3번에 이어서. 물리적인 아이디어의 직접적 구현이 최선은 아니다. 최적화 테크닉이라는 게 있을 법한데 잘 모르겠다. 특정 목적을 달성하는 데 있어서는 동등한 구조를 인식하는 힘. 발산적인 사고를 빠르게 검증하고 확장하는 힘. PS는 재밌다. 하지만 PS가 프로그래밍의 전부는 아니지. 지금 느끼는 도전적임은 실무에서의 도전적임과 다를 것이다. 그곳에는 어떤 성취가 있을지 궁금해진다.

 

5) 그리고 Java 코드가 좀 예쁘지 않은 것 같다. 기능별로 착착 정리해서 분리하고 싶은데 갈피가 잘 안 잡힌다. 지금은 그저 Java의 문법과 친해지는 단계라고 생각한다. OOP 등에 보다 익숙해지면 다른 스타일로 코드를 작성할 수 있겠지?